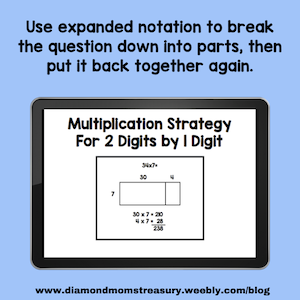
Multiplication Strategies For Kids: Alternatives To Drills

Multiplication is a difficult concept for many children to grasp. Drills are one way to learn, but multiplication strategies will work better. Relating multiplication to what is already known will really help. A simple place to start is by thinking of it as repeated addition.

Strategies To Visualize Multiplication

There are many ways to visualize multiplication. We can use circles and add an equal amount of objects into each one to see that it is grouping things together.

We can use arrays so that we can see the equal rows and columns. Again, we are looking at equal groups, just in a different set up.

We can also actually share objects between people, one for you, one for you, one for you, and so on. This way it is easy to see that they are equal.  The number of objects times the number of people equals the total number of objects.
This could also be a good way to visualize division as the objects are actually being divided equally among the people.

Memorizing multiplication facts used to be the way kids were taught to use multiplication, but many kids didn't understand how this worked and they found memorizing difficult. It is helpful to know multiplication facts, but by also adding some strategies, if they get stuck or don't remember one of the facts, they can still solve the problem.

Sometimes we need to simplify situations so that they make sense. We can't just share an algorithm and expect everyone to be able to do it correctly.
I worked with some grade 5 students that were really struggling with math. They were so confused that they were unable to do the work given in class. We went right back to basic addition facts and how to do addition with larger numbers using some strategies that made sense to them. Once they felt confident with this, we moved on to simple multiplication questions. If multiplication is like repeated addition, it makes sense that they would need to have a solid understanding of addition before moving on to multiplication.

After working on some strategies for single digit multiplication questions, we attempted to do 2 digit times 1 digit questions. By applying the strategies from addition and expanded notation, this process was successful. They were able to see it visually and it finally made sense.

What multiplication strategy should I use?

It is important to remember that not everyone uses the sames strategies to figure out the answer. Just as we all take different routes when we travel to school or downtown, so people take different routes when they solve math questions. As long as the route works and gets you to your destination, that is great. If you have difficulty because you took a wrong turn, it is important to correct that and redirect you. This means that you need to be able to explain your thinking process. I always encourage my students to tell me the route they took.

When I was working with a group of 5 students, it was interesting to hear all the different ways they took to get to their answers. What was especially good, was that the others listened and realized that they didn't have to take the same route, but also, that sometimes the route someone else took might be a better route to try next time. When the route didn't work out, sometimes one of the others was able to explain how to get back on track. This was very exciting. It meant that they were getting it and that they were able to share what they had learned with others.

After practicing strategies for awhile using visuals, it is important to be able to move to a more abstract model. We don't always have materials available to make a visual model. In real life situations, we need to be able to figure things out either mentally or with paper and pencil. This is where the strategies really are useful.

I created a resource that shows some of the strategies and how to use them. If you are interested in checking it out, click the image.

I tutored a couple of girls with these strategies, and it was amazing to see the growth and confidence they had after working with them for awhile. The following year, they went to middle school and the teacher started to give them more difficult material to work with. At first they were confused, but as we broke the material down and looked at it, they were able to see that it was the same process only with larger numbers.
The teacher gave them the traditional algorithm to use and this actually confused them because it wasn't explained. They tried to follow the example but didn't understand what was really happening. When we broke it down and used the strategies they had learned, they figured it out and then they were able to actually use the algorithm. One thing I did tell them was, if you don't get it, use the strategies you know. It may take more space, but it will get you to the right answer. They took this advice and they were able to get through the material.

Not every strategy works with every person. It is important to try them and figure out which ones are the best fit. This will provide a set of tools for real life situations. I hope this has given you some ideas for ways that you can help your students to feel more confident and successful with multiplication.

Here is a simple resource that will help to remind you of some of the strategies to choose from. 

I hope these tips help with teaching your students multiplication. Don't forget to grab your copy of the strategies reference sheets by clicking the image or here. 

For free resources, tips, and ideas, sign up for my newsletter.

Related Posts