Seven Addition Strategies That Help Math Make Sense For Kids

4/9/2023

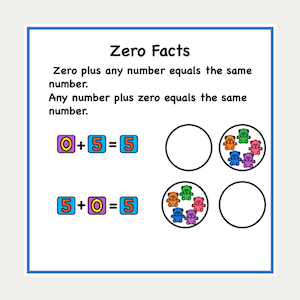
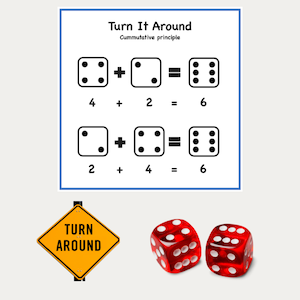
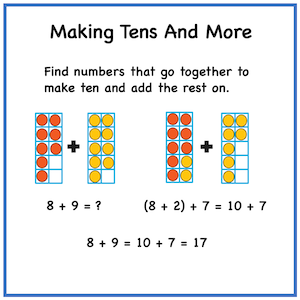
Do you know your basic facts? This may seem like a silly question, but there are many people who struggle with the basics and this is why math is so difficult for them. When I worked with intermediate students that were struggling, I discovered that they were missing the building blocks that would help them with more complex situations. They didn't have a solid foundation and they struggled to find strategies to help.

Math is all around us and it can be frustrating if we don't have a good understanding of how to use it well. As a primary teacher, I know just how important it is to start building strong foundations in math. Learning basic facts is like laying bricks for a sturdy house - without them, the structure can easily crumble.

Fortunately, it is never too late to master the basics and improve math skills. There are many different strategies and approaches available to accomplish this. I would like to focus on a few addition strategies today.

Basic Facts Addition Strategies

Moving from concrete to abstract is important, but first it is necessary to make sure that the foundation of basic facts is solid. Using manipulatives and simple strategies help to make sense of the different concepts, so don't be too quick to remove them as you try out the strategies shown here today.

Adding zero

Adding zero is a concept that can be demonstrated easily with concrete examples. When nothing is added to something, there is no change. As you can see in the example below, it doesn't matter if the zero comes at the beginning of the number sentence or the number of objects comes at the beginning of the sentence, the answer still stays the same.

Turn it around

It's funny how our brains work sometimes. We can figure things out faster when we see a question shown in a certain way. Both of the number sentences below have the same numbers in them, but for some reason it may be easier to recognize the answer faster looking at one of the sentences. That is the beauty of understanding that the cummutative principle of addition means we can turn the question around and still get the correct answer. We may not use the formal term when we teach this strategy, but the visual makes it clear.

Counting on

Counting on is a strategy that is well used for addition. Think of the number of times you may have noticed a child using fingers to count on when figuring out how much more is added. Maybe you have used your fingers to figure things out as well.

Using a number line is another great visual for counting on. Place your pencil (or finger) on the first number in the sentence and count on the number of spaces of the second number to get your answer to the question.

Making tens

Making tens is a great way to help with figuring out addition questions. Start with looking at different ways to make ten using dice, fact families, number bonds, and ten frames.

Making Tens And More

After becoming comfortable with tens you can add in some of the larger numbers to figure out other basic facts.
For example: If you know that 8 + 2 = !0, then for 8 + 9 , you can take 2 from the 9 to make 10 and that leaves 7, so 10 + 7 = 17
See the image below for a visual representation.

Doubles

Learning doubles can be a very helpful strategy. Here are some pictures that can be used as reminders for the doubles for each of the numbers from 1 to 9. There can be other images substituted for these depending on what may work for your students. It will take practice to remember these hints. An anchor chart might also help.

eyes for 1 + 1 : easy to remember because we have 2 eyes
domino with 2 + 2 : counting by twos also works
using dice with 3 + 3 : shows the two rows of 3 dots
spider legs for 4 +4 : spiders have 8 legs
hands for 5+ 5 : counting by fives works as well
carton of eggs for 6 + 6: a dozen is 12
calendar for 7 + 7 : each week has 7 days
2 octopus for 8 + 8 : each one has 8 legs
18 wheeler for 9 + 9 : each side has 9 wheels

Near doubles

Sometimes it helps to use doubles and add one when you need to add two numbers that are close together. For a simple example, check out the image below.

visuals for helping to remember doubles and doubles plus one

Some facts are harder to remember than others. This strategy can work well for some of these situations. For instance, many struggle with 8 + 9. If they double the 8 and add one, it can help.

Here is an addition mandala that is fun to do and helps with practicing basic facts in addition. It comes in both English and French. Get a free copy by signing up for my newsletter.

Get your free mandalas here

There are other strategies that can be used as well, but I wanted to focus on a few tried and true strategies that my students have used.

How to use addition strategies for learning basic facts

Once the basic facts are solid, moving on to more complex addition will be easier. I will share ideas about more complex addition in a future post. For now, I hope that these ideas and strategies help your students to build a strong foundation in math.